我院中国科学院微观磁共振重点实验室杜江峰、荣星等人通过对金刚石量子比特的高精度量子操控,首次在量子体系中实现动力学环绕非厄米奇异点,并成功观测到基于奇异点的本征态转换。该研究成果以“dynamically encircling an exceptional point in a real quantum system”为题,发表在近期的《物理评论快报》上。
近年来,对非厄米量子物理的研究成为了热点,因其不同于传统厄米量子物理,展现出新奇的物理现象,在量子计算、量子精密测量以及拓扑物理等领域有着重要的影响。2019年,杜江峰课题组发展了在量子系统中实现非厄米哈密顿量的普适方法,并在单自旋量子体系中实现了非厄米哈密顿量下的演化[science 364, 878 (2019)],为后续在量子体系中进一步研究非厄米系统的新奇物理性质开辟了道路。
非厄米系统中存在一种特殊的简并点——奇异点。奇异点附近的能谱和厄米系统存在很大的差异,呈现出两个撕裂的黎曼曲面相交环绕着奇异点的特殊拓扑结构(如下图所示),并由此诱导了一些新奇的物理现象。当调控哈密顿量参数,使其动力学地环绕奇异点时,会呈现出拓扑保护的本征态转换。然而,在量子系统中实现这种本征态转换,要求体系在含时非厄米哈密顿量下演化,这非常具有挑战性,因此之前的相关研究均基于经典体系开展模拟实验。
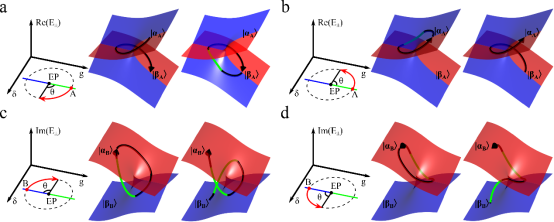
图:奇异点的能谱结构以及动力学环绕奇异点导致的本征态转换。
蓝色和红色曲面分别对应非厄米哈密顿量的两个本征能量,两者在相交的奇异点附近呈现出独特的拓扑结构。
能谱面上带箭头的曲线对应环绕奇异点的演化轨迹。
图a和图b的环绕起点处在宇称时间对称相,呈现出非对称的本征态转换,即末态取决于环绕奇异点的方向,
图c和图d的环绕起点处在宇称时间对称破缺相,呈现出对称的本征态转换,即末态不依赖于环绕奇异点的方向。
研究组基于在量子系统中实现非厄米哈密顿量的普适方法,以金刚石氮-空位色心的核自旋为辅助比特,电子自旋为系统比特,通过量子调控的手段,实现了含时非厄米哈密顿量下的演化,并成功地观测到两种本征态转换。即当环绕的起始点处于宇称时间对称相时,量子系统的末态依赖于环绕奇异点的方向,和环绕初态无关(如图a, b所示),本征态转换呈现出非对称性。而当起始点处于宇称时间对称破缺相时,环绕末态和初态及环绕方向都无关(如图c, d所示),本征态转换呈现出对称性。研究组进一步的探索还发现,这类模式转换对于环绕路径上的随机噪声有很强的鲁棒性,这将在量子计算及量子信息处理领域有重要的应用潜力。
这项工作基于奇异点实现拓扑保护的本征态转换,为量子控制提供了全新的思路。而在量子系统实现含时非厄米哈密顿量,也为进一步研究非厄米系统的新奇物理,如环绕高阶的奇异点、探索非厄米拓扑不变量等奠定了基础。
中国科学院微观磁共振重点实验室博士研究生刘文权和博士后研究员伍旸为该文并列第一作者,杜江峰院士和荣星特任教授为论文的共同通讯作者。此项研究得到了科技部、国家自然科学基金委、中国科学院和安徽省的资助。
论文链接:
(中国科学院微观磁共振重点实验室、物理学院、合肥微尺度物质科学国家研究中心、
中国科学院量子信息和量子科技创新研究院、科研部)
